Задачи с решением
Задача 1.
В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях. Один считает, что первой будет Наташа, а Маша будет второй. Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место. Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй. Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов. Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
Записываем исходную(данную в условии) информацию в виде таблицы:
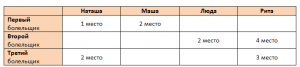
Предполагаем, что Первый болельщик прав и Наташа займет 1-е место:
Так как по условию «каждый из болельщиков был прав только в одном из своих прогнозов», то значит Маша НЕ может занять 2-е место. А также сразу отмечаем что прогноз третьего болельщика «Наташа займет 2-е место» тоже не верный!

По таблице(значения взяты из условия задачи) видим, что 2-е место остается за Людой, так как по условию «каждый из болельщиков был прав только в одном из своих прогнозов», то Рита НЕ может занимать 4-е место.
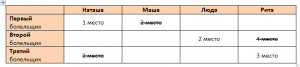
Видим, что Рита будет занимать 3-е место.
В итоге получили, что Наташа займет 1-е место, Люда 2-е место, Рита 3-е место, а Маша займет 4-е.
Снова запишем исходные данные в виде таблицы и разберем другое предположение:

Пусть Маша займет 2-е место. Так как по условию «каждый из болельщиков был прав только в одном из своих прогнозов», значит Наташа не может занимать 1-е место, а также сразу вычеркиваем из высказываний второго и третьего болельщика 2-е место.
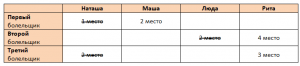
Видим, что теперь получается Рита претендует и на 3-е и на 4-е место, такого быть не может по условию задачи(каждая девушка заняла свое место), значит мы должны вычеркнуть высказывание или второго или третьего болельщика. Вычеркнем высказывание второго болельщика.
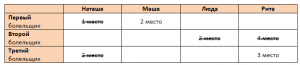
Теперь видим, что НИ ОДИН из прогнозов второго болельщика не оправдался, а этого НЕ может быть по условию задачи. Значит наше предположение что Маша заняла 2-е место — неверно, это тупиковая ветвь рассуждения.
Первое предположение, что Наташа заняла 1-е место, привело нас к ответу, удовлетворяющему всем условиям задачи, соответственно этот ответ считаем ВЕРНЫМ.
Ответ: Наташа займет 1-е место, Люда 2-е место, Рита 3-е место, а Маша займет 4-е.
Задача 2.
В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе.
Известно, что:
1. Смит самый высокий;
2. играющий на скрипке меньше ростом играющего на флейте;
3. играющие на скрипке и флейте и Браун любят пиццу;
4. когда между альтистом и трубачом возникает ссора, Смит мирит их;
5. Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Составим таблицу для решения задачи:

Теперь будем заполнять, в соответствие с исходными данными.
Известно, что Смит самый высокий, но при этом человек, играющий на скрипке меньше ростом играющего на флейте, то есть Смит на скрипке НЕ играет.

Далее известно, что играющие на скрипке и флейте и Браун любят пиццу, из этого условия мы можем сделать вывод, что Браун НЕ играет ни на скрипке, ни на флейте.

Следующее условие «когда между альтистом и трубачом возникает ссора, Смит мирит их» дает нам четкое понимание того, что Смит не играет ни на альте, ни на трубе! ведь нельзя самого себя мирить 🙂

Далее очень простое и всем понятное условие «Браун не умеет играть ни на трубе, ни на гобое.»

По условию задачи «каждый из музыкантов владеет двумя инструментами». Из таблицы видим, что самая заполненная строка, строка музыканта Брауна, содержит как раз 2 пустые ячейки, то есть можно сделать вывод, что Браун умеет играть на альте и кларнете, ставим единички в соответствующие ячейки.

Учитывая то, что музыкантов трое, инструментов шесть, и каждый из них умеет играть только на двух инструментах, получается что каждый музыкант играет на инструментах, которыми остальные не владеют(т.е. их интересы НЕ пересекаются), можем полностью заполнить столбцы, в кторых уже есть по одной единице.

Видим, что строка музыканта Смит содержит пустые ячейки флейта и гобой, на остальных инструментах он играть не умеет, согласно приведенным выше рассуждениям и условиям задачи. Ставим в соответствующие ячейки единицы.
Раз Смит играет на флейте и гобое, то мы понимаем. что Вессон на них играть уже не может и заполняем ячейки нулями.

Теперь из таблицы видно, что Вессон может играть только на скрипке и на трубе.

Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе.